আমরা প্রোগ্রামিং করার সময় খুব বেশি এই প্রশ্ন শুনি যে ‘এই প্রোগ্রামের টাইম কমপ্লেক্সিটি কত?’ একটা প্রোগ্রাম আসলে কী ? আমরা যদি চিন্তা করি দেখবো যে প্রতিটা প্রোগ্রাম / সফটওয়ার কিন্তু আসলে কিছু ফিক্স Operation এর সমষ্টি । তাহলে আমাদের প্রোগ্রাম যখন রান করে তখন এই অপারেশন গুলো চলার জন্য টাইম লাগবে। অপারেশন হতে পারে Assignment operation (a = 2) , conditional operation (a < 0) ইত্যাদি ।
সহজ ভাষায় টাইম কমপ্লেক্সিটি হলো কোনো নির্দিষ্ট ইনপুট এর জন্য একটা প্রোগ্রাম সল্যুশন করতে কত সময় নেয় ।
আমরা জানি যে , কোনো প্রবলেম এর একাধিক সল্যুশন থাকতে পারে। আমি যে কাজ ৫ ঘণ্টায় করতে পারি তুমি সেম কাজ ১ ঘণ্টায় করতেই পারো । তাহলে সময় এর বিবেচনায় তোমার পদ্ধতি আমার চেয়ে ভালো তো আমরা বলবো তোমার সল্যুশন এর টাইম কমপ্লেক্সিটি আমার চেয়ে ভালো ।
একই জিনিস প্রোগ্রামিং এর জন্যেও সত্য । একাধিক সল্যুশন এর মাঝথেকে অপ্টিমাল সল্যুশন খুঁজে বের করার একটা উপায় হচ্ছে তাদের টাইম কমপ্লেক্সিটি বিবেচনা করা। এক্ষেত্রে কিন্তু আমরা এটা বের করছি না যে কত সেকেন্ড সময় লাগলো বরং আমারা কোনও ইনপুট এর জন্য সল্যুশন টাইম এর গ্রোথ রিলেশনটা বের করি । খুবই ভালো কথা আমরা বুঝলাম যে কমপ্লিক্সিটি দেখে আমরা ভালো মন্দ আলাদা করতে পারব তো এখন প্রশ্ন হলো যে এই কমপ্লেক্সিটি আমরা কিভাবে পরিমাপ করব ?
আমাদের মনে হতে পারে যে একই ইনপুট আমরা বিভিন্ন সল্যুশন এর জন্য চালিয়ে ঘড়ি দেখে কত সময় লাগলো তা নোট করে রাখতে পারি। কিন্তু এই প্রসেস এর সমস্যা হলো
- ১। যেই মেশিন এ প্রোগ্রাম রান হচ্ছে তার উপর প্রোগ্রাম এর রানটাইম এর নির্ভর করবে। খুব আপডেটেড একটা পিসি তে যদি একটা খারাপ এলগরিদম রান করে আর একটা পুরুনো কম পাওয়ারের পিসিতে ভালো সল্যুশন রান করে তাহলে তাদের রেসাল্ট ভুল আসবে ।
- ২ । আবার কোনও প্রোগ্রাম হয়তো ১০০ / ১০০০ / ১০০০০ এর জন্য ভালো পারফর্ম করছে কিন্তু ১ কোটি হয়ে গেলে হয়তো আর পারফর্ম করতে পারবে না। তাহলে আমাদের হাতে কলমে এভাবে টেস্ট করাটা আসলে এফিসিয়েন্ট না। আমাদের কোনো প্রসেস লাগবে এর জন্য ।
তাই Algorithm এর Complexity Analysis করার জন্য আমরা Asymptotic Analysis ব্যবহার করি । কোনো এলগরিদমের ইনপুট সাইজ চেঞ্জ হলে সেই ইনপুট এর জন্য সল্যুশন করতে কত টাইম নিচ্ছে সেটাই তার পারফরমেন্স বোঝায়। এখন একটা সল্যুশন এর টাইম কমপ্লেক্সিটি তিনটা অবস্থা হতে পারে যেমন
১। সবচেয়ে কম সময় ( বেস্ট কেস সিনারিও ) – একে ওমেগা নোটেশন ( Ω(n) ) দিয়ে প্রকাশ করা হয়। এটি বেস্ট কেস টাইম কমপ্লেক্সিটি প্রকাশ করে । এটি রিয়েল লাইফে খুব উপকারী কিছু না । ধরি আমাদের একটা ছোটো থেকে বড় সর্ট করা অ্যারে দেয়া আছে আর আমাদের সবচেয়ে ছোটো সংখ্যা বের করার প্রোগ্রাম লিখতে বলেছে। এটা কিন্তু সব সময় প্রথম ইলিমেন্টাই হবে। ইনপুট এর সাইজ যাই হোক এটা কন্সটেন্ট টাইম এ সলভ করতে পারবে । তাহলে বেস্ট কেস এর কমপ্লেক্সিটি হবে Ω(1) কিন্তু রিয়েল লাইফে এমন ইনপুট হবার চান্স খুবই কম ।
২। এভারেজ সময় ( এভারেজ কেস সিনারিও ) – একে থিটা নোটেশন ( Θ(n) ) দিয়ে প্রকাশ করা হয় । এটিও খুব বেশি কাজে লাগে না ।
৩। সবচেয়ে বেশি সময় ( ওরষ্ট কেস সিনারিও ) – একে বিগ ও নোটেশন ( O(n) ) দিয়ে প্রকাশ করা হয় । একে বলা হয় বিগ ও অফ N / অর্ডার অফ N
এটি রিয়াল লাইফে সবচেয়ে বেশি কাজে লাগবে, এর দ্বারা প্রোগ্রামের আপার বাউন্ড জানা যায় , সবচেয়ে বেশি কত সময় লাগবে সেটা জানা যায়। সাধারণত যখন আমরা টাইম কমপ্লেক্সিটি বের করতে বলি আমরা এই ওরস্ট কেস এর জন্য বের করতে বোঝাই । ধরি আমাদের আগের অ্যারেতেই আমাদের একটা নাম্বার খুঁজতে বলা হলো, এক্ষেত্রে সবচেয়ে খারাপ সিনারিও কি হতে পারে ? আমরা পুরো অ্যারে খুঁজে নাম্বারটা পেলাম না মানে সেটা এরেতেই নেই বা সেটা সবার শেষের নাম্বার আর আমরা শুরু থেকে খোঁজা শুরু করেছি। তাহলে এটাই হবে এর সবচেয়ে খারাপ কেস এবং এর কমপ্লেক্সিটি আমরা বলব Big O of n ( O(n) ) যেখানে n অ্যারে এর সাইজ বুঝায়। এর মানে আসলে কি একটু চিন্তা করি । যদি আমাদের ১০০ টা নাম্বার থাকে এবং ধরি একটা নাম্বার চেক করতে ১সেকেন্ড লাগে। তাহলে ১০০ নাম্বার চেক করতে আমাদের প্রোগ্রাম ১০০সেকেন্ড সময় নিবে, ২০০ এর জন্য ২০০ … এভাবে ইনপুট সাইজ আর সময়ের মাঝে একটা লিনিয়ার সম্পর্ক দেখতে পারি ।
তো ভালো কথা আমরা জানলাম যে একটা প্রোগ্রাম এর কমপ্লেক্সিটি অর্ডার অফ এন। এখন এইটা জেনে আমরা কি করতে পারবো ? এর ইমপ্লেকেশন টা কি ?
চলো দেখি …
ধরা যাক আমরা একটা প্রোগ্রাম লিখলাম যেটার ১০০ নাম্বার এর মাঝ থেকে একটা নাম্বার খুঁজতে ৫০০ সেকেন্ড লাগতেসে কিন্তু আমরা এখন জানি যে এটা ১০০ সেকেন্ড এ করা যাবে এমন সল্যুশন ও আছে, তার মানে আমাদের সল্যুশন আরও ইম্প্রুভ করার স্কোপ আছে। আবার ধরি আমাদের আমাদের ১০০ নাম্বারের মাঝে খুঁজতে বলা হলো আর বলে দেয়া হলো ১২০ সেকেন্ড এর মাঝেই প্রোগ্রাম এর এটা খুঁজে বের করতে হবে, তাহলে আমরা বুঝতে পারবও আমাদের লিনিয়ার কোনও সল্যুশন খুঁজতে হবে ।
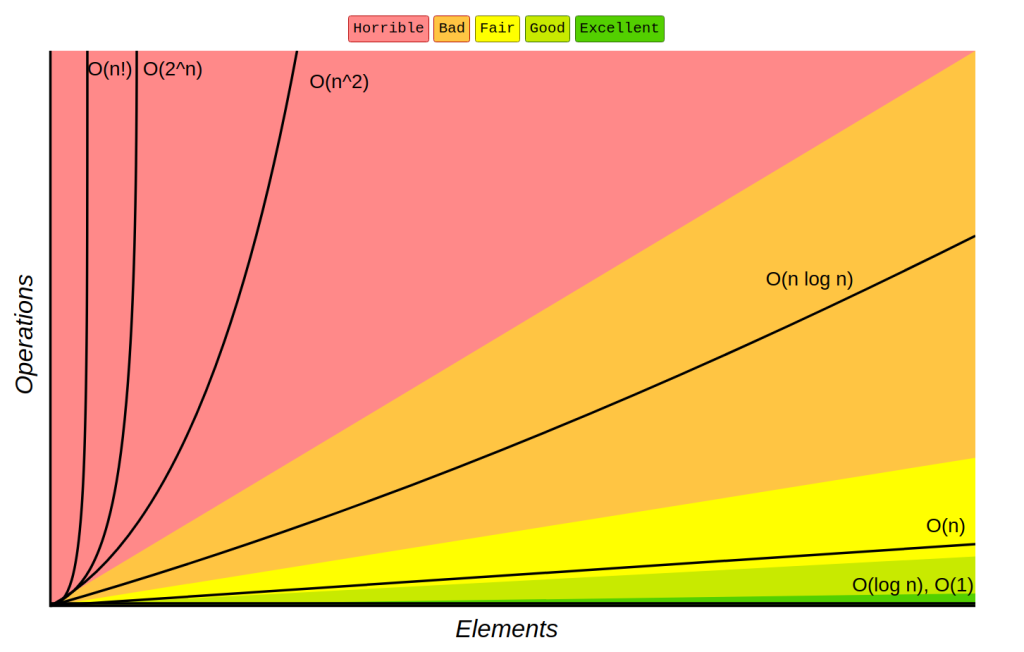
এই চার্টে আমরা দেখতে পারি সবচেয়ে ভালো সল্যুশন হলো কন্সট্যান্ট টাইম কমপ্লেক্সিটির সল্যুশন, তারপর লগারিদ্মিক , পরে লিনিয়ার এভাবে চলতে চলতে শেষে আছে ফ্যাক্টোরিয়াল। এই গ্রাফ টা হলও ইলিমেন্ট বনাম অপারেশন এর গ্রাফ। এর মানে হলো ৫০টা ইলিমেন্ট এর জন্য লিনিয়ার সল্যুশন যখন ৫০টা অপারেশন চালাবে তখন কোয়ার্ডেটিক O(n^2) সল্যুশন O(৫০^২) = ২৫০০ অপারেশন চালাবে আর O(n!)=O(৫০!) হলে … ওয়েল ৫০! এর মান গুগুল করে দেখে নিবেন !!



